class: left, middle, inverse, title-slide # Different Kinds of DIF ## Justifications and Considerations </span> ### --- class: middle # Introduction + "Group" assignment is a Catch-22 in statistics/measurement + Often need to assign people to groups for various reasons + Often have to run the statistical model to make our classifications + Finding important aspects of group membership is a way for us to compare (age-grading, diagnoses, regression modelling) + But what can we do to ensure our group membership, for DIF testing is meaningful? --- class: middle # "Fixed Effects" models + What constitutes a meaningful group? + Consequence - may ignore heterogeneity in treatment effects even within groups + May inflate or a deflate the causual estimate (plus, can you interpret them within group?) + General lesson: A group indicator can induce more problems if not thought through + Problems... --- class: middle # What about relative DIF? + In classroom settings, diagnostic assessment may be of interest and we'd like to compare similar groups + How should we identify groups + we have "observed" groups (or at least we think we do...) + But what happens when the observed groupings (i.e. don't match the goupings we're actually interested in - in the case of DIF)? --- class: middle # Differential Item Functioning (DIF) + Invariance/DIF analysis starts with the premise that items are invariant, when one can, 1. Match respondents on "ability" or a sum score, or the like, 2. Model the responses probabilities to certain items or item categories 3. Note whether the probability of that response to a given item for respondents is the same regardless of group membership --- class: middle # Formalizing Given, participant `i`, item `j`, value on latent trait, `t`, selection variable (or group), `v` `\(F(X_{ij}=x_{ij}|T=t_i, V_i=v_i) = F(X_{ij}=x_{ij}|T=t_i)\)` Non Invariance Occurs when: `\(F(X_{ij}=x_{ij}|T=t_i, V_i=v_i) \neq F(X_{ij}=x_{ij}|T=t_i)\)` --- class: middle # Strategies + Typically, items are removed when measurement non-invariance is found + There are various philosophies: + DIF found: Item removal (no questions asked - testing agencies) + DIF found: Item removal if DIF can be explained + DIF found: Items removed/altered/some parameters are allowed to change --- class: middle # But...An alternative + Absolute and Relative Measurement Invariance + We typically look at absolute invariance + In some cases when absolute non-invariance is found, relative invariance might still hold --- <img src="IOMW_presi_files/figure-html/unnamed-chunk-3-1.png" width="648" style="display: block; margin: auto;" /> --- Absolute DIF `$$P(X_{is}=1|\theta_s, \delta_i, \gamma_i, G_s)=\frac{exp(\theta_s-\delta_i + \gamma_i*G_)}{1+ exp(\theta_s-\delta_i +\gamma_i*G)}$$` <img src="IOMW_presi_files/figure-html/unnamed-chunk-5-1.png" width="648" style="display: block; margin: auto;" /> --- class: middle # Recovering Measurement via Relative Measurement Relative Trait Value: `\(\large z_i = \frac{t_i-\mu_{Tv}}{\sigma_{Tv}}\)` Relative Difficulty: `\(\large \delta_{i_{rel}} = \frac{\delta_{i_{abs}}-\mu_{T_{v}}}{\sigma_{T_{v}}}\)` --- class: middle # Relative Invariance `\(F(X_{ij}=x_{ij}|W=w_i, V_i=v_i) = F(X_{ij}=x_{ij}|W=w_i)\)` Non Invariance Occurs when: `\(F(X_{ij}=x_{ij}|W=w_i, V_i=v_i) \neq F(X_{ij}=x_{ij}|W=w_i)\)` Where `W` is the within group, relative, position ## We've effectively switched units --- class: middle # A reading measure example + Let's say there's an assessment of reading strategy use, we'll call it the SUM (strategy Use Measure) -- + Intended to be multidimensional but treated unidimensionally -- + The assessment has a section testing knowledge of English-Spanish Cognates -- + While the assessment has 157 items, I've cherry picked a set of items that exhibit DIF (for didactic purposes) -- + Note - this is NOT a fair characterization of the assessment --- # I run a Rasch model and find evidence that some items have DIF (I've selected 9 items, some of which show absolute DIF) + Relative measurement not ruled out + I need to test whether I can measure within my "identified" groups + Heritage Spanish Speakers vs. Not heritage Spanish Speakers --- # strategy - trialing a method + Use a clustering method (for instance, latent class analysis) -- + Predict cluster/class membership by subgroup -- + Is there a cluster/class group members are most likely to be part of? Is it as expected based on theory? -- + Compare the cluster/distribution/class shape most like my view of a "group" to what the observed item response proportions -- + Re-estimate the cluster with just the heritage Spanish speakers and just the non-heritage Spanish speakers (English speakers) --- class: middle # Key point **For this to work, I need to have a response process theory in mind** - "Those who read like Spanish Speakers" and "Those who do not" --- ## Key items  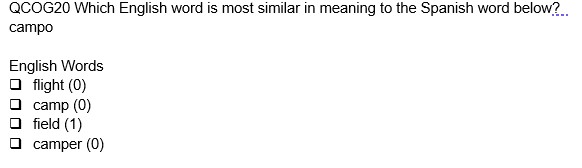 --- class: middle # Data and Methods Description + 328 heritage Spanish Speakers + 999 non-heritage Spanish Speakers + Used Latent Class Analysis + Exploratory Method + Effectively "finds" groups in the data - distributions that are alike + Accept or reject based on fit criteria + Categorical Latent Variable --- <img src="IOMW_presi_files/figure-html/unnamed-chunk-7-1.png" width="720" style="display: block; margin: auto;" /> --- <img src="IOMW_presi_files/figure-html/unnamed-chunk-8-1.png" width="720" style="display: block; margin: auto;" /> --- class: middle, center # Structural Model  --- class: middle ## Methods + Probability of being in a given class given self-identified heritage language + Multinomial logistic regression + Reference Outcome: Class 3 - the "Spanish reading profile" + Reference of the Language Predictor: non-heritage Spanish Speakers --- class: middle ## Results + Compared to non-heritage Spanish Speakers, those who identify as heritage Spanish Speakers are 3 logits less likely to be in the class 1 and class 2. + Flipping the reference classes and language groups around: + Students who are Spanish at home Speakers are 3 logits more likely to be in reference class 3 (Spanish at home) than any other class relative to non-Spanish at home speakers + 3 logits ~ 95% + -3 logits ~ 5% --- class: middle ## That's promising for relative measurement + But let's think about that - it's not 100% -- + What do the profiles look like when I run an LCA without each group? + Model without heritage Spanish speakers + Model with heritage Spanish speakers --- <img src="IOMW_presi_files/figure-html/unnamed-chunk-9-1.png" width="720" style="display: block; margin: auto;" /> --- <img src="IOMW_presi_files/figure-html/unnamed-chunk-10-1.png" width="720" style="display: block; margin: auto;" /> --- # Final Not Spanish Speakers Compared to full final model .pull-left[ 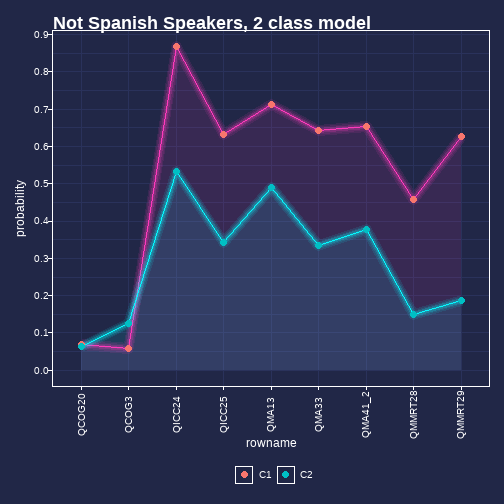<!-- --> ] .pull-right[ <!-- --> ] --- ## Just Spanish Compared to Final Model .pull-left[ <!-- --> ] .pull-right[ 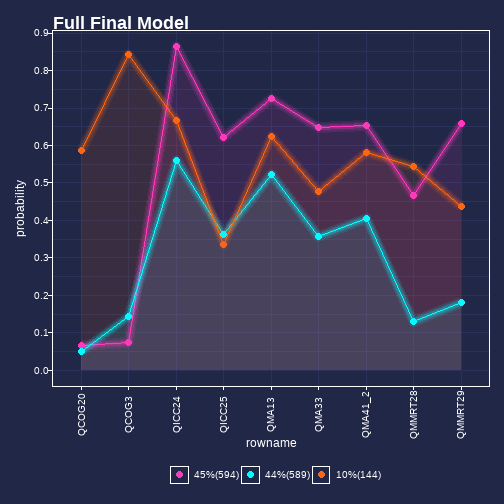<!-- --> ]